Physics-based Machine Learning
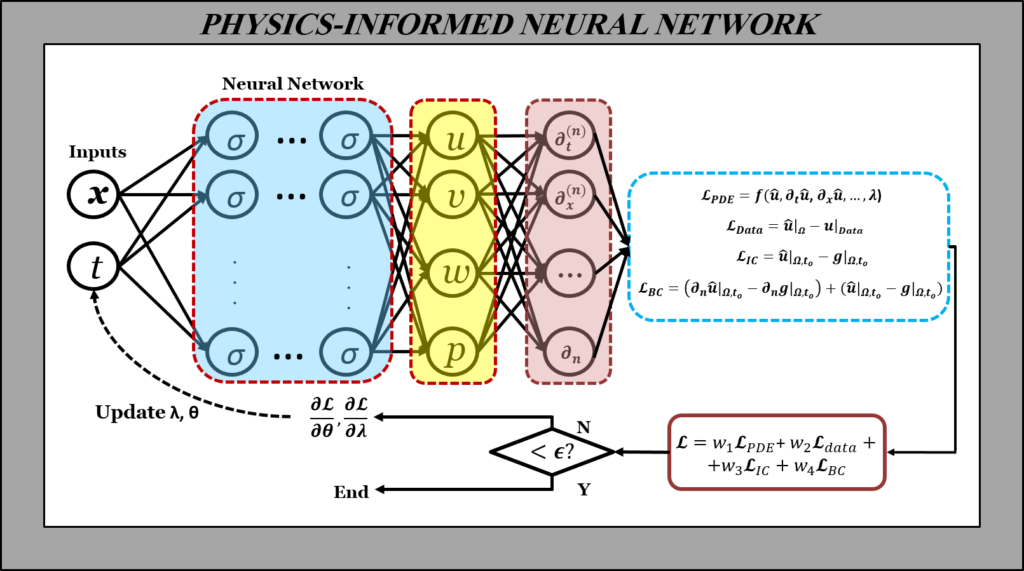
One of the key procedures of this Physics-Informed Neural Network (PINN) is to construct a PDE loss function by computing the partial derivatives using automatic differentiation (AD). In PINN, solving a PDE system is converted into an optimization problem by iteratively updating trainable parameters with the goal to minimize the loss function. Generally, we use the ADAM optimizer, an adaptive algorithm for gradient-based first-order optimization, to optimize the model parameters.
PINN uses automatic differentiation to represent all the differential operators and hence there is no explicit need for a mesh generation. Instead, the Navier–Stokes equations and any other kinematic or thermodynamic constraints can be directly incorporated in the loss function of the neural network (NN) by penalizing deviations from the target values (e.g., zero residuals for the conservation laws) and are properly weighted with any given data, e.g., partial measurements of the surface pressure. The computation of partial derivatives can be calculated with an explicit expression, hence avoiding introducing discretization and truncation errors in conventional numerical methods. A multitask learning problem is defined in order to simultaneously fit observed data while respecting the underlying governing laws of physics.
Transient computational fluid dynamics (CFD)

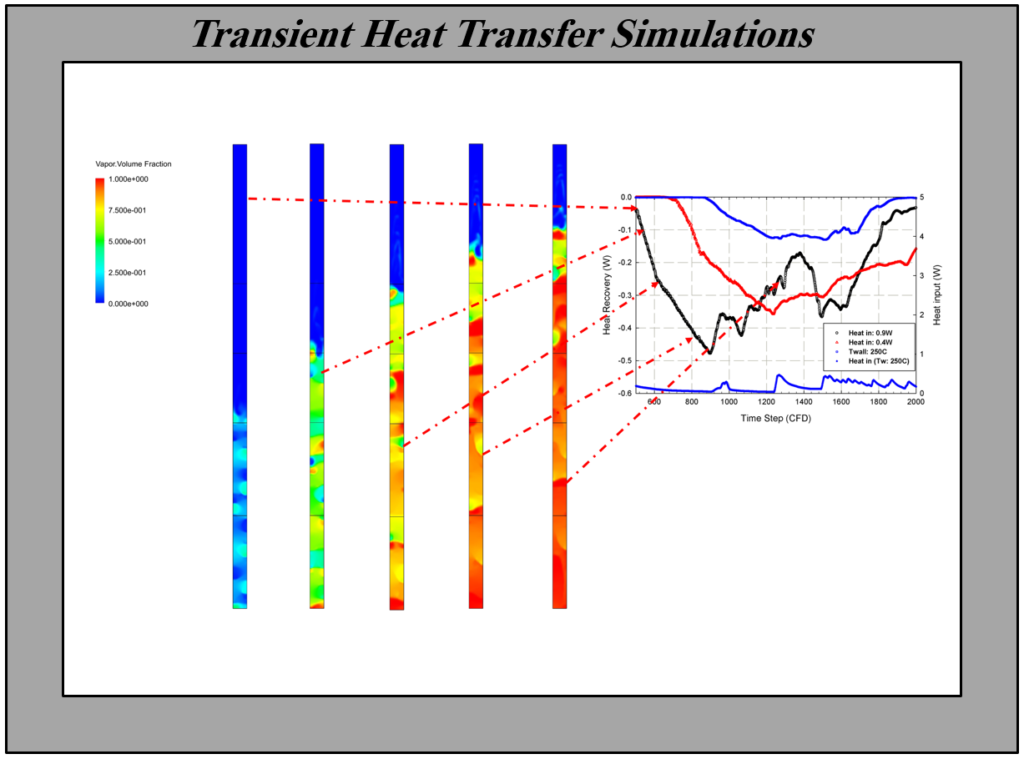
Large Eddy Simulations (LES) were conducted to capture the flow dynamics inside a piping system. The computational domain was divided into sub-domains. Grid refinement was performed in regions of high pressure/velocity gradients and predicted locations of shocks. In addition, grid adaptation based on pressure/velocity gradients was used in order to achieve acceptable grid size ranges in important regions of the domain. Boundary layer mesh refinement was used close to the walls. A second order upwind scheme was chosen for the spatial discretization of the convective terms and the QUICK method was selected for the discretization of the turbulent equations.
The OpenFoam package was used to implicitly solve the governing equations using a transient RANS model. The Volume of Fluid (VOF) technique has been applied for the modelling of a closed two-phase thermosyphon by determining the motion of all phases and defining the motion of the interfaces indirectly from the numerical results. The governing equations of mass continuity, momentum and energy (Navier–Stokes equations) were solved simultaneously. A 3-D geometry with specific grids near the walls was provided for modeling of flow, heat and mass transfer within the thermosyphon. The evaporator, condenser and adiabatic sections were modelled.